Mean Squared Error (MSE) Cost Function

Explore the significance of Mean Squared Error (MSE) cost function in model evaluation and optimization. This comprehensive article delves into its definition, types, advantages, limitations, and applications across various fields. Gain insights into its computational mechanics and strategic integrations to enhance predictive modeling in 2025 and beyond.

Mean Squared Error (MSE) Cost Function: A Cornerstone Metric for Model Evaluation and Optimization 📊

In the domain of statistical analysis and machine learning, the mean squared error (MSE) serves as a fundamental cost function, quantifying the disparity between predicted and actual values to guide algorithmic refinement. This metric, prized for its mathematical elegance and interpretability, underpins regression tasks by penalizing deviations proportionally to their magnitude, thereby fostering models that minimize predictive inaccuracies.

As of October 2025, with advancements in neural networks and predictive analytics amplifying its relevance, MSE remains a staple in evaluating everything from financial forecasting to climate simulations. This article provides a comprehensive overview, encompassing its conceptual foundations, computational mechanics, illustrative applications, advantages and limitations, comparative analyses, and strategic integrations, offering a precise resource for data scientists and analysts seeking to harness its full potential.

Definition

For n samples: MSE-cost=n1​i=1∑n​(y^​i​−yi​)2

• y^​i​ = predicted value
• yi​ = true value

Average of squared differences between predicted (ŷ) and true (y) values.

Why “Cost”?

• Convex for linear models → global minimum guaranteed.
• Penalises large errors quadratically → drives weights toward smaller residuals.
• Everywhere differentiable → smooth gradient for SGD / Adam / LBFGS.

Types of MSE Cost Functions – 2025 Quick Map

Although the core MSE formula is always
  MSE = 1/n Σ (ŷᵢ − yᵢ)²,
practitioners adapt, weight or regularise it to handle outliers, imbalance, sparsity or streaming data. Below are the most common variants you’ll meet in libraries and papers.

1. Plain / Classical MSE

• No weights, no regularisation.
• Use: baseline regression, well-behaved residuals.

2. Weighted MSE (WMSE)

  WMSE = 1/n Σ wᵢ (ŷᵢ − yᵢ)²

• wᵢ > 1 for high-leverage or rare samples; wᵢ < 1 for noisy observations.
• sklearn: sample_weight argument in LinearRegression, SGDRegressor.

3. Huberised MSE (Pseudo-Huber)

  Lδ = Σ [ δ² (√(1 + ((ŷ−y)/δ)² ) − 1) ]

• Smooth transition between MSE (small errors) and MAE (large errors).
• δ = inflection point (hyper-parameter).
• Robust to outliers yet differentiable.

4. Trimmed / Winsorised MSE

• Discard or cap the top/bottom 5 % of residuals before squaring.
• Keeps convexity while removing outlier influence.

5. Root Mean Squared Error (RMSE)

  RMSE = √MSE

• Same optimum as MSE (monotonic transform).
• Units = target variable → easier interpretation.

6. MSE with L2 (Ridge) Penalty

  L(θ) = MSE + λ‖θ‖₂²

• Shrinks coefficients; handles multicollinearity.
• Closed-form exists; convex.

7. MSE with L1 (Lasso) Penalty

  L(θ) = MSE + λ‖θ‖₁

• Sparse solutions (feature selection).
• Non-differentiable at 0 → coordinate descent or proximal methods.

8. Elastic-Net MSE

  L(θ) = MSE + λ₁‖θ‖₁ + λ₂‖θ‖₂²

• Blends Lasso + Ridge; selects grouped variables; p > n survival.

9. Group Lasso MSE

  L(θ) = MSE + λ Σ_g √|g| ‖θ_g‖₂

• Selects/deselects whole factor groups (e.g., all dummy levels of a categorical).

10. Adaptive / Weighted Lasso MSE

  L(θ) = MSE + λ Σ w_j |θ_j| where w_j = 1 / |θ̂_j|^γ

• Data-driven weights → oracle property (asymptotically correct selection).

11. Quantile MSE (check-function)

  Lτ = Σ [ (y−ŷ)(τ − 1_{y<ŷ}) ]

• Minimises τ-quantile, not mean; robust to outliers; no Gaussian assumption.

12. Heteroskedasticity-Corrected MSE

• Weights inversely proportional to estimated variance σ̂²(x).
• Iteratively re-weighted least squares (IRLS).

13. Online / Streaming MSE

• Recursive least squares or SGD with forgetting factor.
• Constant-time update; suitable for IoT / high-frequency data.

14. Fair MSE (Fair-loss)

  L = Σ [ c² |e|/c − log(1 + |e|/c) ]

• Smooth, robust, less severe than Huber for large errors.

15. ε-Insensitive MSE (SV Regression)

  L = 0 if |e| < ε; otherwise (|e| − ε)²

• Ignores small errors → sparse solution (support vectors).

🔑 How to Choose

Situation	Pick
Clean, normal errors	Plain MSE or RMSE
Outliers present	Huber, Fair, Quantile, Trimmed
High multicollinearity	Ridge (L2)
Feature selection needed	Lasso, Elastic-Net, Adaptive Lasso
Streaming / big data	SGD, Online MSE, Recursive Least Squares

Conceptual Foundations: Purpose and Role in Predictive Modeling 📈

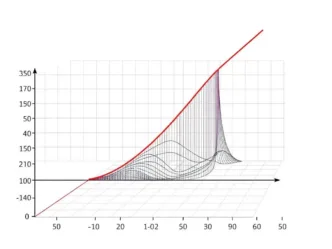
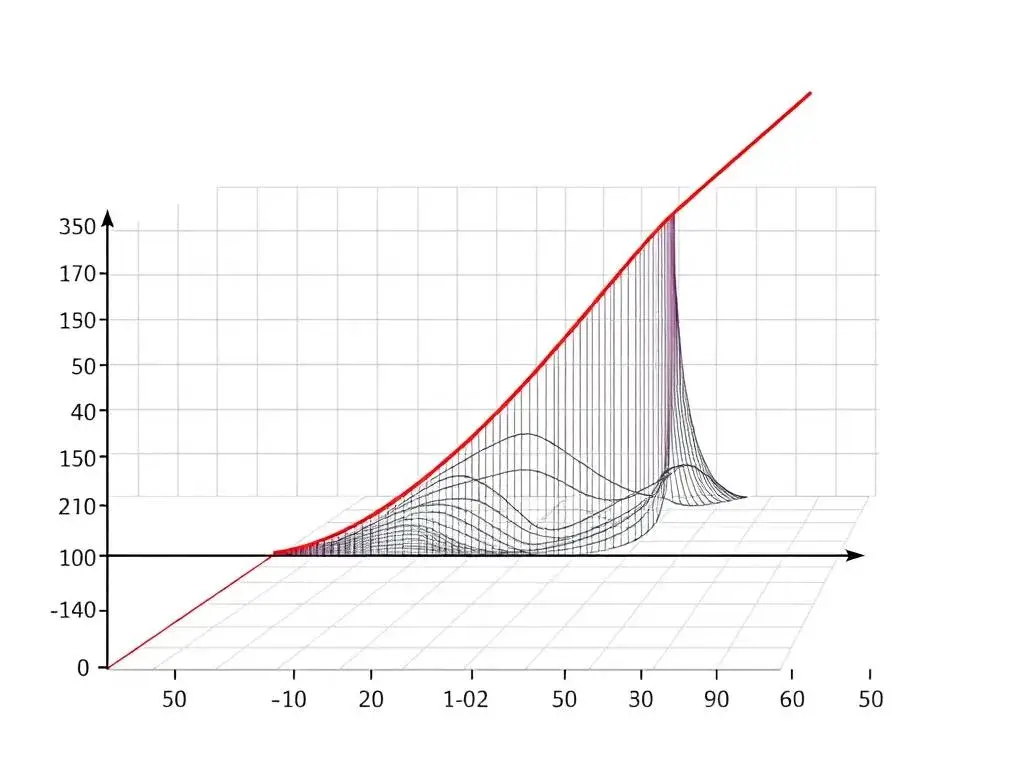
Mean squared error (MSE) cost embodies the essence of regression evaluation, measuring the average squared difference between observed outcomes and model forecasts. Its primary objective is to encapsulate prediction error in a single, differentiable scalar, enabling gradient-based optimization in algorithms like linear regression or deep learning frameworks.

By squaring residuals, MSE accentuates larger deviations—ensuring that outliers exert greater influence on model adjustments—while its mean aggregation normalizes for dataset size, yielding a scale-dependent yet comparable metric. In practical terms, MSE transforms raw discrepancies into actionable feedback, guiding iterative improvements toward empirical fidelity.

Computational Mechanics: Formula and Derivation 🔢

The MSE is articulated through a concise formula: MSE = (1/n) ∑(y_i – ŷ_i)^2, where n denotes the number of observations, y_i represents the actual value, and ŷ_i the predicted counterpart for the i-th instance. Computation proceeds in three steps: first, calculate individual residuals (y_i – ŷ_i); second, square them to eliminate directional bias and emphasize magnitude; third, average the results to derive the error rate.

For instance, envision a dataset of housing prices: actual values [200, 250, 300] thousand dollars contrast with predictions [210, 240, 310]. Residuals yield [ -10, 10, -10 ], squared to [100, 100, 100], and averaged to 100—indicating, on average, a 10 thousand-dollar deviation per unit squared. This derivation, rooted in least squares estimation, facilitates closed-form solutions in ordinary least squares regression, underscoring MSE’s analytical tractability.

Illustrative Applications: MSE in Diverse Domains 🌍

MSE’s versatility manifests across sectors, illuminating its adaptability. In finance, it evaluates portfolio models by comparing forecasted returns against historical yields, refining risk assessments for algorithmic trading. Healthcare leverages MSE to calibrate diagnostic algorithms, minimizing errors in patient outcome predictions—e.g., a model estimating blood glucose levels might achieve an MSE of 15 mg/dL², signaling clinical viability.

Environmental science employs it for climate projections, where MSE quantifies discrepancies between simulated temperature anomalies and observed data, guiding refinements in global circulation models. In e-commerce, recommendation engines use MSE to optimize personalized suggestions, reducing average rating deviations from 0.5 to 0.2 stars, enhancing user satisfaction.

These applications highlight MSE’s role as a universal evaluator, bridging theoretical precision with empirical impact.

✅ MSE Cost Function – Advantages & Disadvantages (2025)

Aspect	Advantage	Disadvantage
Mathematical Nature	Convex → global minimum guaranteed	Outlier-sensitive (squaring magnifies large residuals)
Differentiability	Everywhere differentiable → smooth gradient for GD, SGD, Adam	Biased toward smaller errors; large errors dominate
Closed-Form Solution	Normal equation exists (no learning-rate tuning)	Units squared → harder to interpret than MAE (same units as target)
Convergence Speed	Fast convergence for well-conditioned data	Slow / unstable if Hessian is ill-conditioned or outliers skew surface
Robustness	Optimal for Gaussian noise (MLE justification)	Non-robust for heavy-tailed or contaminated data
Computational Cost	Vectorisable (one matrix multiply)	Scales poorly with very large n or high-dimensional sparse data
Regularisation Friendly	L2 penalty adds analytically, keeps problem convex	L1 regularisation loses differentiability at 0 → requires sub-gradient methods

Advantages: Strengths in Simplicity and Optimization 🚀

MSE’s merits are manifold: its convexity ensures a unique global minimum, simplifying convergence in optimization routines like stochastic gradient descent. Differentiability supports seamless backpropagation in neural networks, while familiarity among practitioners expedites adoption. Scale sensitivity proves advantageous in homogeneous datasets, where uniform error magnitudes align with domain tolerances, and its quadratic penalty incentivizes robust models less prone to wild inaccuracies.

Limitations: Considerations for Robust Implementation ⚠️

Despite its strengths, MSE harbors constraints. Sensitivity to outliers can skew results, as a single anomalous data point disproportionately inflates the metric, potentially leading to overfitted models. Scale dependence complicates cross-dataset comparisons—e.g., an MSE of 100 in price predictions dwarfs one of 0.01 in probability estimates—necessitating normalization via root mean squared error (RMSE) for interpretability. Moreover, it assumes homoscedastic errors, faltering in heteroscedastic scenarios like financial volatility, where alternative metrics may prevail.

🔑 Rule of Thumb

• Switch to Huber, MAE, or quantile loss if large outliers are part of the data-generating process.
• Use MSE when errors are roughly normal and outliers are rare/correctable.

Comparative Analyses: MSE in Context with Peers ⚖️

Relative to mean absolute error (MAE), MSE’s squaring amplifies large errors, suiting precision-critical applications like engineering tolerances, whereas MAE’s linearity favors median-aligned robustness in noisy data. Against log-loss in classification, MSE’s continuous focus suits regression, but log-loss’s probabilistic grounding excels in binary outcomes. Huber loss hybridizes these, blending MSE’s penalization with MAE’s outlier resistance, offering a tunable alternative for contaminated datasets. These contrasts position MSE as a baseline, with hybrids addressing its outlier vulnerabilities.

Strategic Integrations: Enhancing MSE in Modern Workflows 🔗

To maximize efficacy, integrate MSE with ensemble methods like random forests, where aggregated predictions dilute individual variances, or cross-validation to mitigate overfitting. In 2025’s AI ecosystem, tools such as TensorFlow or Scikit-learn automate MSE computations within pipelines, pairing it with visualization libraries like Matplotlib for error heatmaps. For enterprise deployment, embed MSE in dashboards via Tableau, correlating it with business KPIs to inform real-time recalibrations.

Prospective Developments: MSE in an AI-Augmented Future 🔮

As machine learning matures, MSE will evolve alongside federated learning paradigms, aggregating errors across decentralized datasets for privacy-preserving models. Quantum computing may accelerate its optimization in high-dimensional spaces, while explainable AI integrations will unpack squared contributions, demystifying black-box decisions. In sustainability analytics, MSE could quantify carbon footprint forecasts, aligning predictive accuracy with global imperatives.

Bottom line:

MSE is the mother loss—tune it, weight it, penalise it, or robustify it to match your data’s quirks and business constraints.

MSE = smooth, fast, globally solvable—but demands outlier scrutiny; pair with robust diagnostics or alternative losses when heavy tails appear.

In conclusion, mean squared error (MSE) cost, through its rigorous quantification of predictive fidelity, stands as an indispensable metric that not only evaluates but elevates model sophistication. Its quadratic insight, tempered by judicious application, empowers analysts to bridge data with destiny, ensuring forecasts illuminate rather than obscure. For tailored implementations or extensions to related metrics, further professional dialogue is encouraged.